
| ||||
| auteur : Thibaut Cuvelier | ||||
La fonction Solve[] est ici d'un grand secours. C'est elle qui permet de résoudre une équation, donnée en premier paramètre, en fonction de la
variable passée en second paramètre. Étant donné que la résolution est symbolique, elle peut se faire pour n'importe quel symbole apparaissant dans l'équation.
Il est évidemment possible de résoudre des équations avec moins de paramètres :
Comme annoncé, on peut résoudre cette première équation pour une autre variable que l'habituel x :
En la variable a, l'équation quadratique devient une simple équation linéaire, d'où la solution.
Il est aussi possible de ne récupérer qu'une seule solution, par exemple la seconde :
Évidemment, cela n'est possible que pour des équations acceptant autant de solutions.
|
| ||
| auteur : Thibaut Cuvelier | ||
La fonction Solve[] est toujours appropriée. Elle peut aussi prendre un troisième argument, en plus de l'expression de l'équation et de
la variable à considérer, qui est le domaine sur lequel il faut chercher des solutions.
|
| ||
| auteur : Thibaut Cuvelier | ||
La fonction Solve[] est aussi d'un grand secours. Elle peut aussi résoudre des équations pour plusieurs variables, par exemple :
Il est aussi possible de résoudre des systèmes non linéaires :
La sortie texte n'est pas forcément la plus lisible par un humain, voici donc le rendu sous forme d'image :
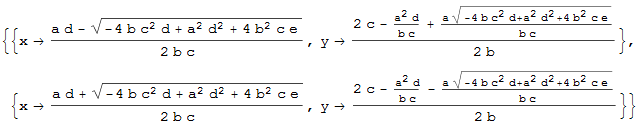 |
| ||
| auteur : Thibaut Cuvelier | ||
La fonction Solve[] sert pour toutes les résolutions d'équations algébriques (pas pour les équations différentielles ou aux différences),
mais aussi pour les inéquations algébriques. On peut les utiliser pour réduire l'ensemble des solutions possibles à un problème. Par exemple :
À plusieurs variables, cela peut aussi donner des résultats intéressants :
|
| |||
| auteur : Thibaut Cuvelier | |||
La fonction Solve[] n'est en réalité utile que lorsqu'il n'y a qu'une solution ou un ensemble de solutions, pas une infinité de solutions.
Rentrent dans cette catégorie les inéquations. On utilise alors la fonction Reduce[], qui réduit une ou plusieurs expressions en
aussi peu que possible.
À plusieurs variables, cela peut aussi donner des résultats intéressants :
On peut aussi user de fonctions transcendantes :
|
| ||
| auteur : Thibaut Cuvelier | ||
La fonction DSolve[] se charge de la résolution symbolique des équations différentielles, autant en systèmes que simples.
Elle prend trois paramètres : l'expression de la ou des équations, la fonction inconnue et la variable indépendante.
|
| ||||
| auteur : Thibaut Cuvelier | ||||
La fonction RSolve[] se charge de la résolution symbolique de telles équations.
Elle prend trois paramètres : l'expression de la ou des équations, la fonction inconnue et la variable indépendante.
On peut aussi poser des conditions initiales au problème :
|
| |||
| auteur : Thibaut Cuvelier | |||
Cette fois, il faut utiliser la fonction NSolve[], où N est un préfixe pour indiquer la résolution numérique.
On peut résoudre de simples équations polynomiales, les solutions ne devant pas forcément être réelles :
Mathematica faisant surtout du calcul symbolique, on pourrait essayer de mélanger les deux (on n'obtiendra pas exactement les mêmes
résultats que pour une résolution purement symbolique, même si elles sont mathématiquement équivalentes) :
Pour cette dernière commande, la sortie est suffisamment longue pour ne pas être recopiée ici.
On peut toujours demander à restreindre les solutions à un certain intervalle, à résoudre un système d'équations, etc.
La syntaxe est la même que pour une résolution symbolique.
|
| |||
| auteur : Thibaut Cuvelier | |||
À cette fin, on utilise la fonction FindRoot[]. Elle sert tant pour des équations à une seule inconnue
qu'à plusieurs
À chaque fois, il faut préciser une première estimation de la valeur de chaque variable, afin de converger vers une solution intéressante. Par exemple,
si on avait précisé une tout autre valeur pour la première équation, le résultat aurait pu être totalement différent :
|
| ||
| auteur : Thibaut Cuvelier | ||
Cette fois, il faut utiliser la fonction NDSolve[]. Elle peut résoudre des équations différentielles
dans un certain intervalle pour une certaine variable, le retour est une fonction interpolée. On va dans cet exemple
utiliser la fonction retournée pour en afficher un graphique :
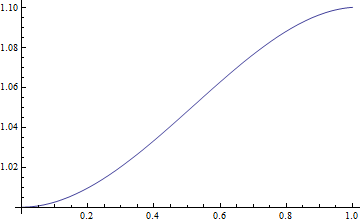
Notez que l'on doit fournir autant de conditions initiales que nécessaire pour obtenir une et une seule solution
(un problème de Cauchy, autrement dit), soit autant de conditions que l'ordre de l'équation. Sinon, la solution
ne sera pas unique et la résolution numérique ne pourra pas se faire. Ce problème est inhérent à l'analyse
numérique.
On peut ensuite aussi récupérer des valeurs précises, même en dehors de l'intervalle de résolution de l'équation.
Une extrapolation sera alors effectuée, les résultats ne seront pas précis, Mathematica vous préviendra dans ce cas.
On peut aussi résoudre des systèmes d'équations différentielles ordinaires avec cette fonction ; à titre documentaire,
sachez qu'il est toujours possible de transformer une équation différentielle d'ordre n en un système
de n équations différentielles du premier ordre, ce qui simplifie grandement la résolution numérique.
|
| ||
| auteur : Thibaut Cuvelier | ||
La fonction NDSolve[] en est toujours capable.
 |
Copyright © 2011 Thibaut Cuvelier. Aucune reproduction, même partielle, ne peut être faite de ce site ni de l'ensemble de son contenu : textes, documents, images, etc. sans l'autorisation expresse de l'auteur. Sinon vous encourez selon la loi jusqu'à trois ans de prison et jusqu'à 300 000 € de dommages et intérêts.